最近做了这道题，附上链接

这道题文字很多，不易读

题目描述

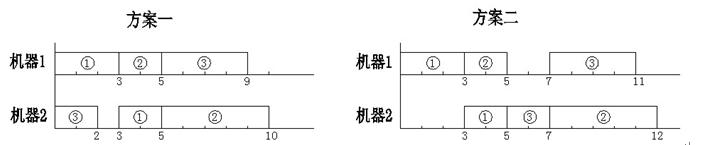
我们现在要利用

m台机器加工n个工件，每个工件都有m道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。 每个工件的每个工序称为一个操作，我们用记号j-k表示一个操作，其中j为1到n中的某个数字，为工件号；k为1到m中的某个数字，为工序号，例如2-4表示第2个工件第4道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。 例如，

当n=3，m=2时，“1-1，1-2，2-1，3-1，3-2，2-2”就是一个给定的安排顺序，即先安排第1个工件的第1个工序，再安排第1个工件的第2个工序，然后再安排第2个工件的第1个工序，等等。 一方面，每个操作的安排都要满足以下的两个约束条件。

(1) 对同一个工件，每道工序必须在它前面的工序完成后才能开始； (2) 同一时刻每一台机器至多只能加工一个工件。 另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。 由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为“1 1 2 3 3 2”。 还要注意，“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。 例如，取n=3,m=2，已知数据如下： 

 则对于安排顺序“1 1 2 3 3 2”，下图中的两个实施方案都是正确的。但所需要的总时间分别是10与12。 　 当一个操作插入到某台机器的某个空档时（机器上最后的尚未安排操作的部分也可以看作一个空档），可以靠前插入，也可以靠后或居中插入。为了使问题简单一些，我们约定：

在保证约束条件（1）（2）的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件（1）（2）的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。 显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。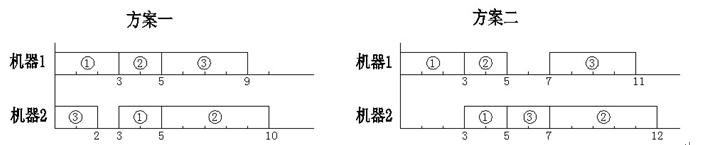

 

输入

第1行为两个正整数m和n（其中m（<20）表示机器数，n（<20）表示工件数），用一个空格隔开：第2行：个用空格隔开的数，为给定的安排顺序。接下来的2n行，每行都是用空格隔开的m个正整数，每个数不超过20。其中前n行依次表示每个工件的每个工序所使用的机器号，第1个数为第1个工序的机器号，第2个数为第2个工序机器号，等等。后n行依次表示每个工件的每个工序的加工时间。

输出

只有一个正整数，为最少的加工时间。

样例输入

2 31 1 2 3 3 21 2 1 2 2 13 2 2 5 2 4

样例输出

10 以上就是题目的内容 解题： 题目主要内容为红字部分

我的理解就是给了我们工件数n；机器数m；加工工件的顺序安排worklist[n*m]；以1~n的顺序，每个工件在加工时按工序的排列workmac[工件编号][工序号]；

以1~n的顺序,每个工件在加工时按workmac顺序花费的时间worktime[工件编号][工序号]；整理如下：

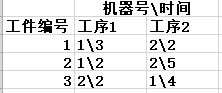
从题目和上面的三张图来看，我们需要得到花费时间最少的方案，按我们人的想法，就是尽可能（不违背（1）（2）约定）的让机器1和机器2工作，别闲着。所以需要找机器1和机器2时间线timeline[机器号][时间数]的空闲处，见可容纳的空余就插入。

1.按worklist（给定顺序）的顺序开始，找到当前加工的工件号nowitem（这样不会违背我们的约定）；

2.当前工件进行到哪一步啦？当然是上一步+1了，step[nowitem]++；

3.这个工件应该在机器workmac[nowitem][step[nowitem]]上面加工；

4.加工时间是worktime[nowitem][step[nowitem]]；

5.我们从机器workmac[nowitem][step[nowitem]]的时间线的最开始的头部1，一点点的加，找到一段可以容纳worktime[nowitem][step[nowitem]]的位置，作为当前工件当前工序的加工时间，并标记这段时间。

6.最后会得到每个工件加工完在时间线上的时间点，找到最后加工完的那个工件，即时间点最大的工件

代码如下：

#include
      
       #define MAX 21int nowitem;//当前的工件编号 int worklist[MAX*MAX];//工件加工给定顺序int workmac[MAX][MAX];//【工件编号，工件工序号】机器编号int worktime[MAX][MAX];//【工件编号，工件工序号】花费时间int lasttime[MAX];//【工件编号】每个工件最后做完时间 int timeline[MAX][10000];//【机器编号，时间线长度】 int step[MAX];//当前编号工件进行到的工序 ，初始时都为0 int check(int st,int end,int mac){    //找是否有空余的位置     for(int i=st;i<=end;i++)    {        if(timeline[mac][i]==1)        return 0;    }    return 1;}int main(){    int n,m;     scanf("%d %d",&m,&n);     for(int i=1;i<=n*m;i++)     {         scanf("%d",&worklist[i]);     }     for(int i=1;i<=n;i++)     {         for(int j=1;j<=m;j++)         {             scanf("%d",&workmac[i][j]);         }     }     for(int i=1;i<=n;i++)     {         for(int j=1;j<=m;j++)         {             scanf("%d",&worktime[i][j]);         }     }     int mac,costtime;     for(int i=1;i<=n*m;i++)     {         nowitem=worklist[i];//当前安排工件编号          step[nowitem]++; //工序号加一        mac=workmac[nowitem][step[nowitem]];//机器号        costtime=worktime[nowitem][step[nowitem]];//花费时间        for(int t=lasttime[nowitem]+1;;t++)        {            if(check(t,t+costtime-1,mac)==1)            {                for(int j=t;j<=t+costtime-1;j++)                {                    timeline[mac][j]=1;                }                lasttime[nowitem]=t+costtime-1;                break;            }         }            }     int maxtime=-1;     for(int i=1;i<=n;i++)     {         if(lasttime[i]>maxtime)         maxtime=lasttime[i];     }     printf("%d\n",maxtime);    return 0;}
      

 参考：https://blog.csdn.net/wsnbb123456789/article/details/49508119